最有趣、最危险、最复杂的世界数学难题,一个
【作者】网站采编
【关键词】
【摘要】来玩个游戏吧…… 选择任意正整数。如果是奇数,则乘以3,加1。如果是偶数,则除以2。对得到的新数进行同样的处理,并继续这样做。如果你在某个时候得到了数字 1,那就停下来。
来玩个游戏吧……
选择任意正整数。如果是奇数,则乘以3,加1。如果是偶数,则除以2。对得到的新数进行同样的处理,并继续这样做。如果你在某个时候得到了数字 1,那就停下来。
我知道这可能不是世界上最有趣的游戏,但请玩一会儿。我向你保证这会很有趣。
例如,如果我们从7开始,我们会得到如下序列(从现在开始,我们称之为Colac序列)。
- 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. li> ul>
- 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.
如果我们从 19 开始,我们得到:
请注意,在某些时候,我们在上述两个序列中都有数字 22,因此它们“尾巴”也是一样。
问题是:我们总是以1结束吗?
信不信由你,上面的问题是一个很深的谜。尽管许多非常聪明的数学家付出了巨大的努力,但这个问题仍然没有得到解决。
这个问题叫做“科拉兹猜想”。
陷入混乱
但为什么这么难理解?毕竟,孩子会明白这个游戏的规则。它看起来非常简单。
通过对小数的Kolatz数列的初步观察,我们没有看到什么意外的情况,但是当我们到达的时候,比如数字27,对应的数列是111步,它之前达到了9232迅速下降到 1。
如果我们绘制 27 的 Colats 序列,我们将得到以下图表。
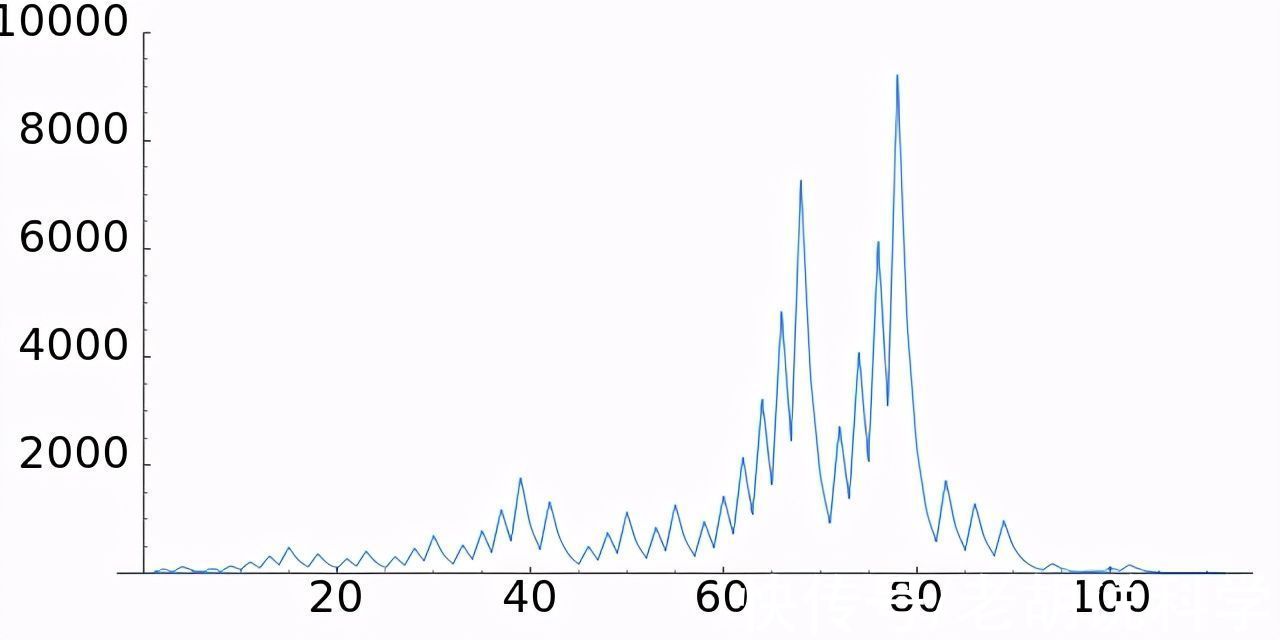
这个看起来有点随机,其实这个问题有点随机,哪个使其难以处理。我们稍后会讨论这个问题。
请注意,如果n是奇数,那么3n+1就是偶数,我们需要将它除以2,这样我们就可以将这两步合二为一,简单来说就是(3n+ 1)/2。
当我们把上面两个步骤结合起来时,我们将得到的序列称为简化的Kolatz序列。
考虑下面的函数。
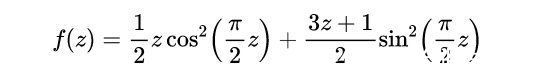
这个函数会输出简化后的Kolatz序列中的下一个数字,当然,前提是z是一个整数。
但是这个函数,如果我们在复平面上定义它,就是一个完备的函数,也就是说我们可以给它输入任何复数,而且它是复可微的。
Mark Chamberlain 在实线上研究了这个函数的迭代,发现这导致了一个动态系统。他证明了这个猜想并不适用于所有正实数,因为有无限多个不动点和轨道。
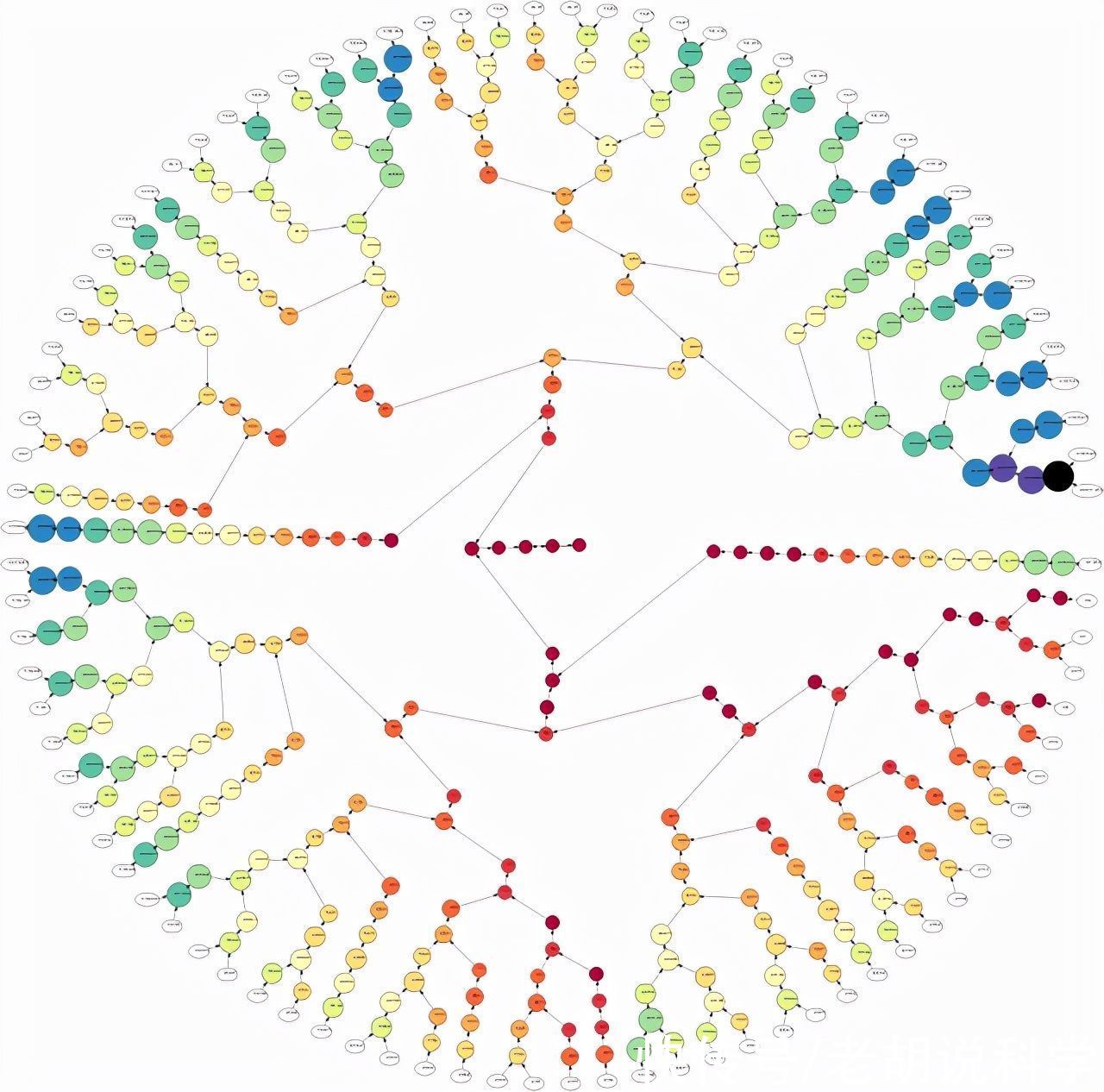
您可以在下面看到相应的美丽的 Kolatz 分形。

这说明这些系列确实有一些内在的混乱。
众所周知,动态系统和分形源于混沌系统,例如天气。决定性的特征是系统对初始条件极其敏感。
对于我们的问题,这意味着考虑整数和实数之间存在巨大差异。即使我们可以通过实数序列任意逼近给定的整数,对应的柯拉兹序列也可能有很大的不同。这引起了混乱。
解决方案
那么,解决方案是什么样的?我们需要证明两件事。首先,我们需要证明所有序列都是有界的。换句话说,不存在无限的 Kolatz 序列。我所说的无限意味着序列中的数字集是无限的。其次,我们需要证明循环是不可能的。换句话说,在 Kolatz 序列中,我们永远不会遇到一个数字两次。如果我们从1开始,那么4、2、1的序列就会无限重复。
当然还有另一种解决方案。这个猜想可能是错误的。数学家试图验证,起始值大约是2^68。 1958年,波利亚猜想(波利亚猜想)改为约1.845×10^361被反例推翻,这比2^68的数字大很多。
实际上,这里可能会发生另一件事。数学家通常不谈论这个问题,因为这是一个非常可悲的想法。科拉茨猜想在我们的公理系统中可能是无法解决的,也就是说,无论我们怎么努力,也无法破解它。
不要被问题的美丽所迷惑
那么为什么这是一个危险的问题呢?
因为,当你试图解决一个数学问题而你不知道是否能解决它时,你花费了所有宝贵的时间,最后却一无所获。
时间是最宝贵的,它在数学中非常容易使用,尤其是当一个问题看起来很简单的时候。但实际上一点也不简单。这就像希腊神话中的塞壬。
希腊神话中的海妖原本是一群形似美女,实则是会吃人的野兽。他们坐在岸边,用迷人的声音唱歌。任何听到它们的人都会为它们着迷。然后塞壬会吃掉它们。
这个问题很像这样。它看起来如此美丽和简单,但在你意识到之前,你已经花费了多年的研究和精力,最终还是一无所获。
文章来源:《生物数学学报》 网址: http://www.swsxxb.cn/zonghexinwen/2021/0909/558.html